## Списки
Сигнатура для стека
```
signature Stack = sig
type α Stack
val empty : α Stack
val isEmpty: α Stack -> bool
val cons : α x α Stack -> α Stack
val head : α Stack -> α Stack /* возбуждает EMPTY для пустого стека */
val tail : α Stack -> α Stack /* возбуждает EMPTY для пустого стека */
end
```
Реализация стека с помощью встроенного типа списков
```
structure List : Stack = structure
type α Stack = α list
val empty = []
fun isEmpty s = null s
fun cons (x, s) = x::s
fun head s = hd s
fun tail s = tl s
end
```
Одна часто встречающаяся операция на списках: ++, которая конкатенирует (т. е., соединяет) два списка. Эту функцию нетрудно поддержать за время
O(1), если сохранять указатели и на первый, и на последний элемент списка. Тогда ++ просто изменяет последнюю ячейку первого списка так, чтобы
она указывала на первую ячейку второго списка. Обратите внимание, что эта операция уничтожает оба своих аргумента после выполнения xs ++ ys ни xs, ни ys использовать больше нельзя.
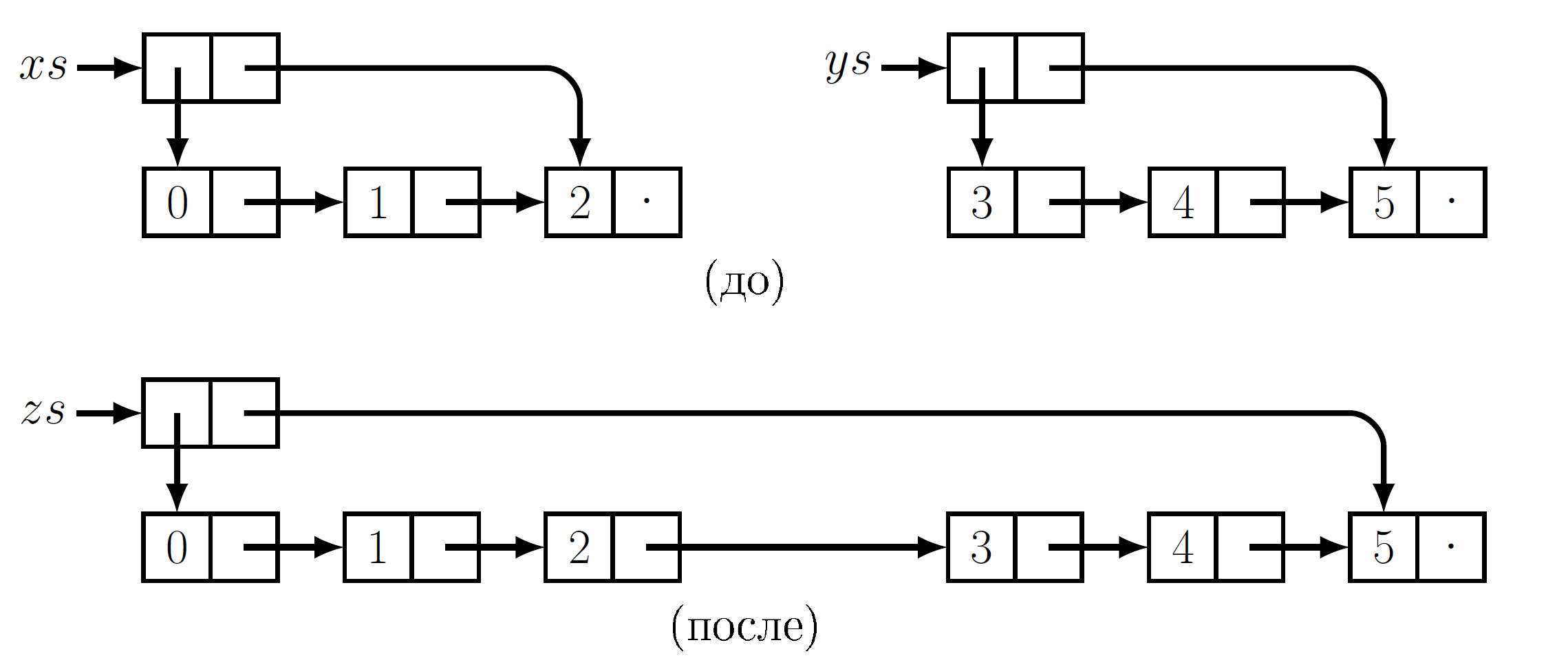
Выполнение xs++ys в императивной среде. Эта операция уничтожает списки-аргументы xs и ys.
В функциональном окружении мы не можем деструктивно модифицировать последнюю ячейку первого списка. Вместо этого мы копируем эту ячейку и модифицируем хвостовой указатель в ячейке-копии. Затем мы копируем предпоследнюю ячейку и модифицируем ее хвостовой указатель, указывая на копию последней ячейки. Такое копирование продолжается, пока не окажется скопирован весь список. Процесс в общем виде можно реализовать как
```
fun xs++ys = if isEmpty xs then ys else cons (head xs, tail xs++ys)
```
Обратите внимание, что после выполнения операции конкатенации мы можем продолжать использовать два исходных списка, xs и ys. Таким образом, мы добиваемся устойчивости, но за счет копирования ценой O(n)
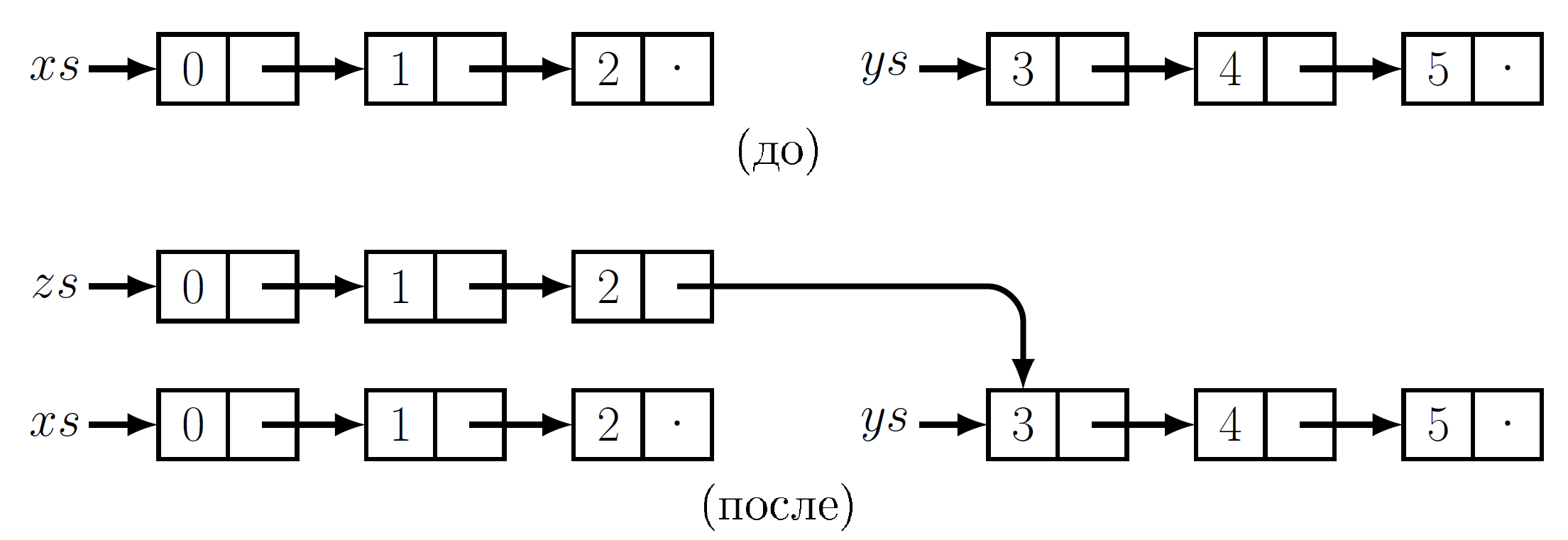
Несмотря на большой объем копирования, заметим, что второй список, ys, нам копировать не пришлось. Эти узлы теперь общие между ys и zs. Еще одна функция, иллюстрирующая парные понятия копирования и общности подструктур update, изменяющая значение узла списка по данному
индексу.
```
fun update ( [ ] , i , y) = raise Subscript
| update (x : : xs , 0, y) = y : : xs
| update (x : : xs , i , y) = x : : update(xs , i-1, y)
```
Здесь мы не копируем весь список-аргумент. Копировать приходится только сам узел, подлежащий модификации (узел i) и узлы, содержащие прямые или косвенные указатели на i. Другими словами, чтобы изменить один узел, мы копируем все узлы на пути от корня к изменяемому. Все узлы, не находящиеся на этом пути, используются как исходной, так и обновленной версиями. На Рис. 3 показан результат изменения третьего узла в пятиэлементном списке: первые три узла копируются, а последние два используются совместно.
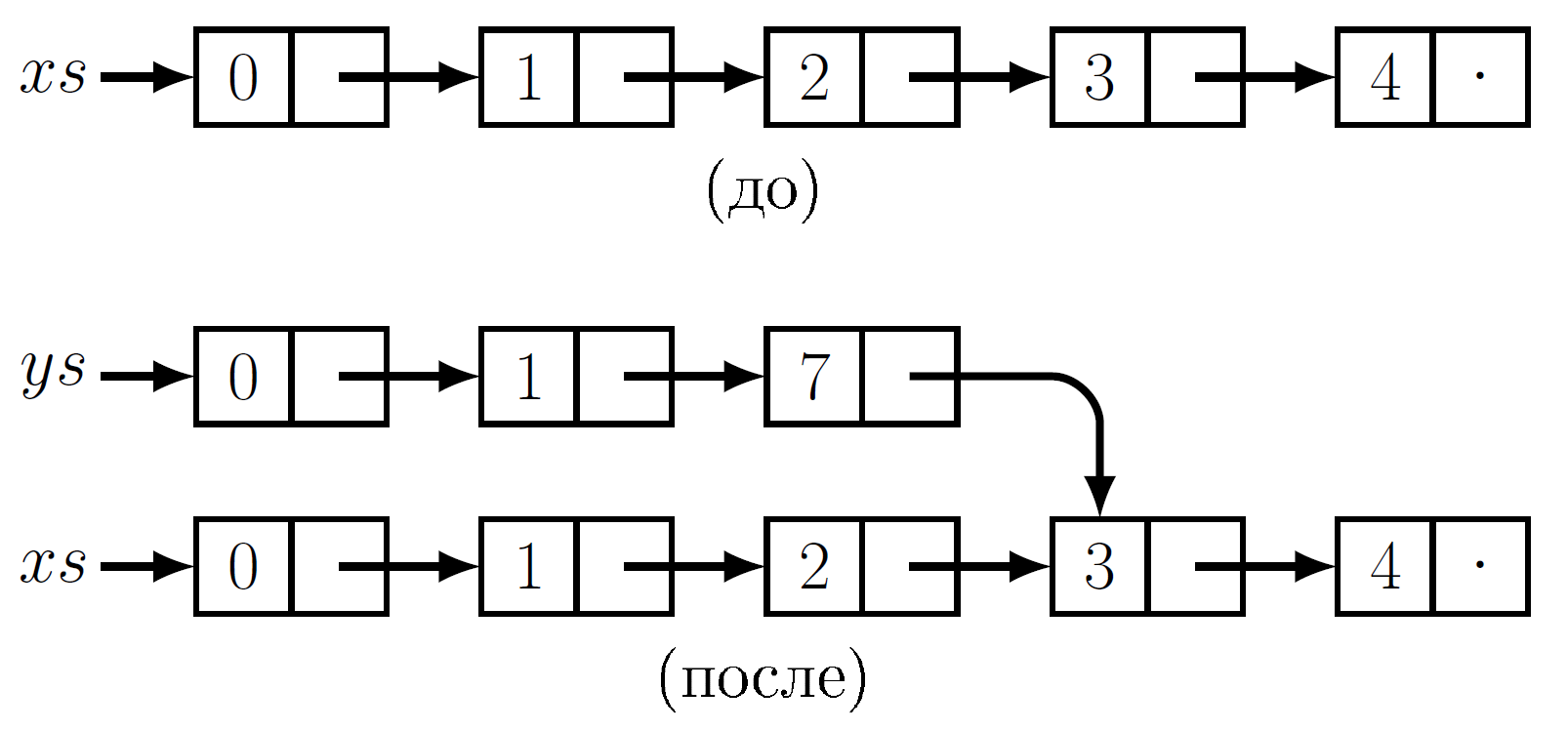
Выполнение ys =update(xs, 2, 7). Обратите внимание на совместное использование структуры списками xs и ys.
Прим.
Такой стиль программирования очень сильно упрощается при наличии автоматической сборки мусора. Очень важно освободить память от тех копий, которые больше не нужны, но многочисленные совместно используемые узлы делают ручную сборку мусора нетривиальной задачей.
## Двоичные деревья поиска
Если узел структуры содержит более одного указателя, оказываются возможны более сложные сценарии совместного использования памяти. Хорошим примером совместного использования такого вида служат двоичные деревья поиска.
Двоичные деревья поиска это двоичные деревья, в которых элементы
хранятся во внутренних узлах в симметричном (symmetric) порядке, то
есть, элемент в каждом узле больше любого элемента в левом поддереве
этого узла и меньше любого элемента в правом поддереве. В Стандартном
ML мы представляем двоичные деревья поиска при помощи следующего
типа:
```
datatype Tree = E | T of Tree x Elem x Tree
```
где Elem какой-либо фиксированный полностью упорядоченный тип элементов.
Прим.
Двоичные деревья поиска не являются полиморфными от-
носительно типа элементов, поскольку в качестве элементов не может
выступать любой тип подходят только типы, снабженные отношени-
ем полного порядка. Однако это не значит, что для каждого типа элемен-
тов мы должны заново реализовывать деревья двоичного поиска. Вместо
этого мы делаем тип элементов и прилагающиеся к нему функции срав-
нения параметрами функтора (functor), реализующего двоичные деревья
поиска.
Мы используем это представление для реализации множеств. Однако
оно легко адаптируется и для других абстракций (например, конечных
отображений) или поддержки более изысканных функций (скажем, найти
i-й по порядку элемент), если добавить в конструктор T дополнительные
поля.
Сигнатура для множеств
```
signature SET = sig
type Elem
type Set
val empty : Set
val insert : Elem x Set -> Set
val member : Elem x Set -> bool
end
```
Сигнатура содержит значение "пустое множество", а также функции добавления нового элемента и проверки на членство. В более практической реализации, вероятно, будут присутствовать и многие другие функции, например, для удаления элемента или перечисления всех элементов.
Функция member ищет в дереве, сравнивая запрошенный элемент с находящимся в корне дерева. Если запрошенный элемент меньше корневого,
мы рекурсивно ищем в левом поддереве. Если он больше, рекурсивно ищем
в правом поддереве. Наконец, в оставшемся случае запрошенный элемент
равен корневому, и мы возвращаем значение "истина". Если мы когда-либо
натыкаемся на пустое дерево, значит, запрашиваемый элемент не является членом множества, и мы возвращаем значение "ложь". Эта стратегия
реализуется так:
```
fun member(x,E) = false
j member(x,T(a,y,b)) =
if x < y then member(x,a)
else i f x > y then member(x,b)
else true
```
Функция insert проводит поиск в дереве по той же стратегии, что и
member, но только по пути она копирует каждый элемент. Когда наконец
оказывается достигнут пустой узел, он заменяется на узел, содержащий
новый элемент.
```
fun insert (x,E) = T(E,x,E)
| insert (x, s as T(a,y,b)) =
if x < y then T( insert (x,a) ,y,b)
else if x > y then T(a,y, insert (x,b))
else s
```
На Рис. 4 показана типичная вставка. Каждый скопированный узел использует одно из поддеревьев совместно с исходным деревом; речь о том поддереве, которое не оказалось на пути поиска. Для большинства деревьев путь поиска содержит лишь небольшую долю узлов в дереве. Громадное большинство узлов находятся в совместно используемых поддеревьях.
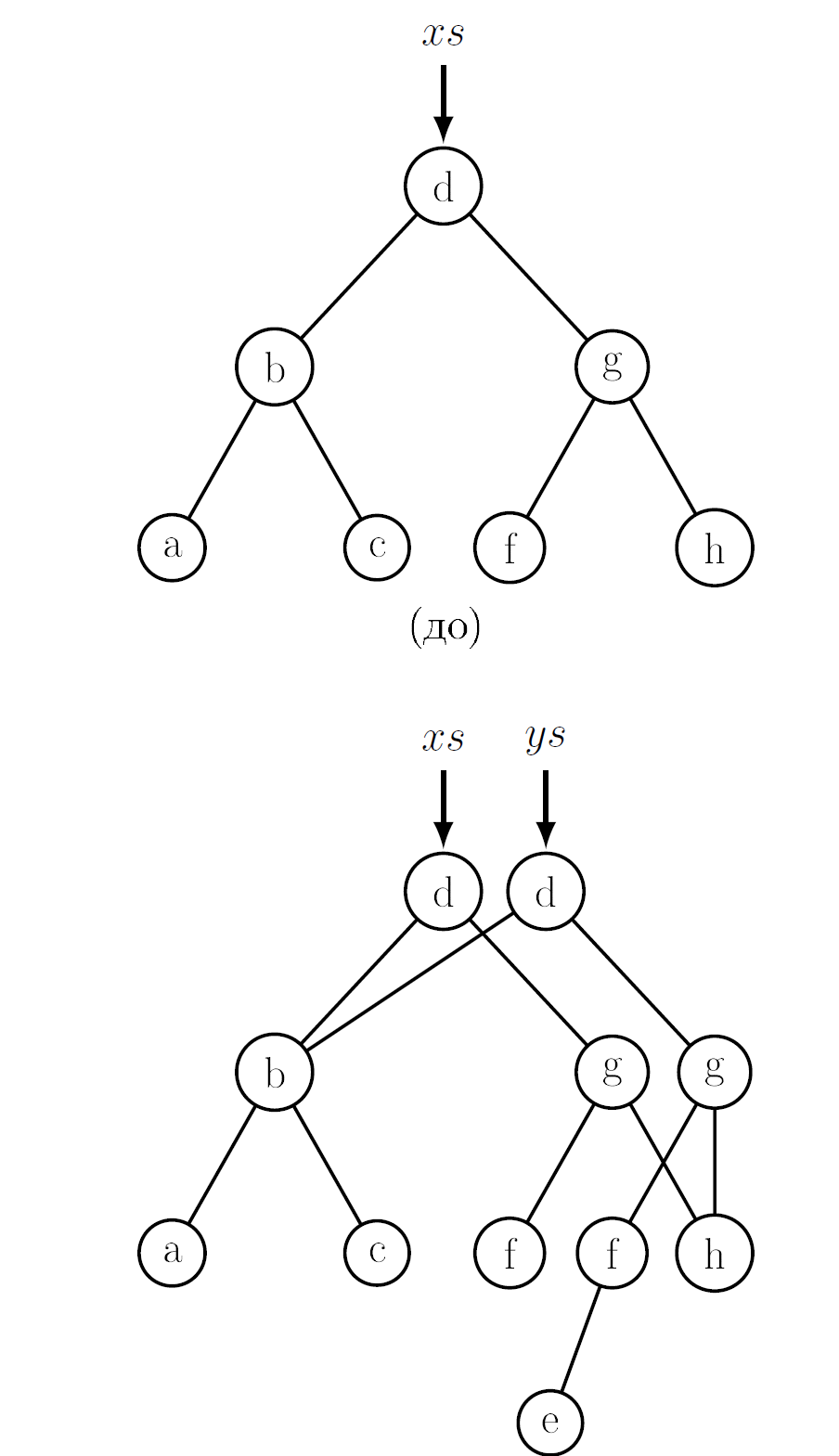
Выполнение ys = insert ("e", xs). Как и прежде, обратите внимание на совместное использвание структуры деревьями xs и ys.
### Левоориентированные кучи
Как правило, множества и конечные отображения поддерживают эффективный доступ к произвольным элементам. Однако иногда требуется эф
фективный доступ только к минимальному элементу. Структура данных, поддерживающая такой режим доступа, называется очередь с приоритетами (priority queue) или куча (heap). Чтобы избежать путаницы с очередями FIFO, мы будем использовать второй из этих терминов.
```
signature HEAD= sig
structure Elem: ORDERED
type Heap
val empty : Heap
val isEmpty : Heap -> bool
val insert : Elem.T x Heap -> Heap
val merge : Heap x Heap -> Heap
val findMin : Heap -> Elem.T /*возбуждает EMPTY при пустой куче */
val deleteMin : Heap -> Elem.T /*возбуждает EMPTY при пустой куче */
end
```
Сравнивая сигнатуру кучи с сигнатурой множества, мы видим, что для кучи отношение порядка на элементах включено в сигнатуру, а для множества нет. Это различие вытекает из того, что отношение порядка играет важную роль в семантике кучи, а в семантике множества не играет. С другой стороны, можно утверждать, что в семантике множества большую роль играет отношение равенства, и оно должно быть включено в сигнатуру.
Часто кучи реализуются через деревья с порядком кучи (heap-ordered),
т. е., в которых элемент при каждой вершине не больше элементов в под-
деревьях. При таком упорядочении минимальный элемент дерева всегда
находится в корне.
### Левоориентированные кучи
Левоориентированные кучи представляют собой двоичные деревья с порядком кучи, обладающие свойством левоориентированности (leftist property): ранг любого левого поддерева не меньше ранга его
сестринской правой вершины. Ранг узла определяется как длина его правой
периферии (right spine) (т. е., самого правого пути от данного узла до пу-
стого). Простым следствием свойства левоориентированности является то,
что правая периферия любого узла кратчайший путь от него к пустому
узлу.
Если у нас есть некоторая структура упорядоченных элементов Elem,
мы можем представить левоориентированные кучи как двоичные деревья,
снабженные информацией о ранге.
```
datatype Heap = E | T of int x Elem.T x Heap x Heap
```
Заметим, что элементы правой периферии левоориентированной кучи (да
и любого дерева с порядком кучи) расположены в порядке возрастания.
Главная идея левоориентированной кучи заключается в том, что для сли-
яния двух куч достаточно слить их правые периферии как упорядоченные списки, а затем вдоль полученного пути обменивать местами поддеревья
при вершинах, чтобы восстановить свойство левоориентированности. Это
можно реализовать следующим образом:
```
fun merge (h, E) = h
| merge (E, h) = h
| merge (h1 as T(_, x, a1 , b1 ) , h2 as T(_, y, a2 , b2 )) =
if Elem. leq (x, y) then makeT (x, a1 , merge (b1 , h2 ))
else makeT (y, a2 , merge (h1 , b2 ))
```
где makeT вспомогательная функция, вычисляющая ранг вершины T и,
если необходимо, меняющая местами ее поддеревья.
```
fun rank (E) = 0
| rank (T (r , _, _, _)) = r
fun makeT (x, a, b) = if rank a >= rank b then T (rank b +1, x, a, b)
else T (rank a + 1, x, b, a)
```
Поскольку длина правой периферии любой вершины в худшем случае ло-
гарифмическая, merge выполняется за время O(log n).
Теперь, когда у нас есть эффективная функция merge, оставшиеся функ-
ции не представляют труда: insert создает одноэлементную кучу и сливает
ее с существующей, ndMin возвращает корневой элемент, а deleteMin отбра-
сывает корневой элемент и сливает его поддеревья.
```
fun insert (x, h) = merge (T (1 , x, E, E) , h)
fun findMin (T (_, x, a, b)) = x
fun deleteMin (T (_, x, a, b)) = merge (a, b)
```
Поскольку merge выполняется за время O(log n), столько же занимают и insert с deleteMin. Очевидно, что findMin выполняется за O(1).
### Биномиальная куча
Биномиальные очереди, которые мы, чтобы избежать путаницы с очередями FIFO, будем называть биномиальными кучами (binomial heaps) еще одна распространенная реализация куч. Биномиальные кучи устроены сложнее, чем левоориентированные, и, на первый взгляд, не возмещают эту сложность никакими преимуществами. Однако в последующих главах мы увидим, как в различных вариантах биномиальных куч можно заставить insert и merge выполняться за время O(1).
Биномиальные кучи строятся из более простых объектов, называемых
биномиальными деревьями. Биномиальные деревья индуктивно определя-
ются так:
* Биномиальное дерево ранга 0 представляет собой одиночный узел.
* Биномиальное дерево ранга r+1 получается путем связывания (linking) двух биномиальных деревьев ранга r, так что одно из них становится самым левым потомком второго.