Биномиальные очереди, которые мы, чтобы избежать путаницы с очередями FIFO, будем называть биномиальными кучами (binomial heaps) еще одна распространенная реализация куч. Биномиальные кучи устроены сложнее, чем левоориентированные, и, на первый взгляд, не возмещают эту сложность никакими преимуществами. Однако в последующих главах мы увидим, как в различных вариантах биномиальных куч можно заставить insert и merge выполняться за время O(1).
Биномиальные кучи строятся из более простых объектов, называемых биномиальными деревьями. Биномиальные деревья индуктивно определяются так:
* Биномиальное дерево ранга 0 представляет собой одиночный узел.
* Биномиальное дерево ранга r+1 получается путем связывания (linking) двух биномиальных деревьев ранга r, так что одно из них становится самым левым потомком второго.
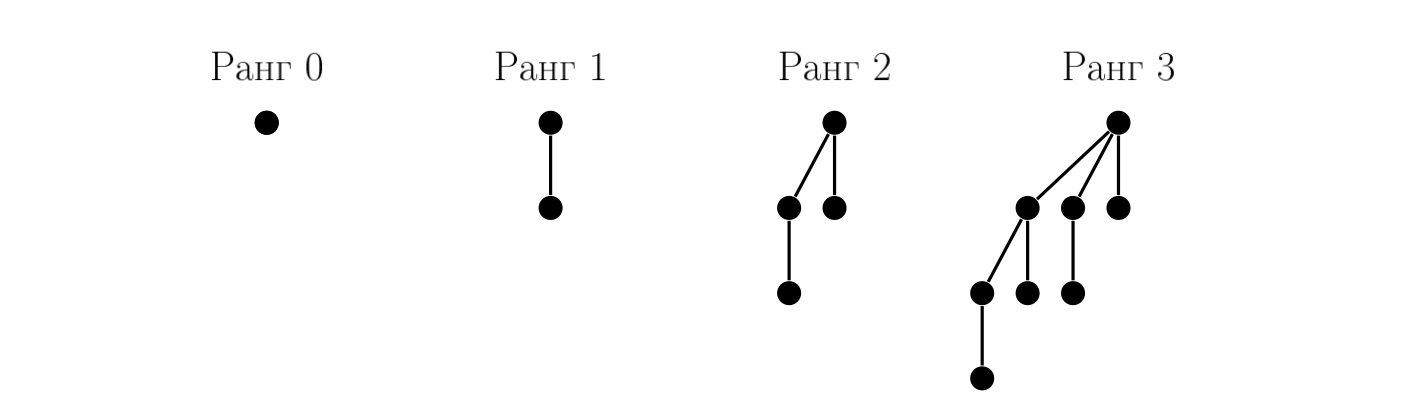
Из этого определения видно, что биномиальное дерево ранга r содержит ровно 2r элементов. Существует второе, эквивалентное первому, определение биномиальных деревьев, которым иногда удобнее пользоваться: биномиальное дерево ранга r представляет собой узел с r потомками t1 . . . tr , где каждое ti является биномиальным деревом ранга r-i. На Рис. показаны биномиальные деревья рангов от 0 до 3.
Мы представляем вершину биномиального дерева в виде элемента и списка его потомков. Для удобства мы также помечаем каждый узел его рангом.
```
datatype Tree = Node of int x Elem.T x Tree list
```
Каждый список потомков хранится в убывающем порядке рангов, а элемен- ты хранятся с порядком кучи. Чтобы сохранять этот порядок, мы всегда привязываем дерево с большим корнем к дереву с меньшим корнем.
```
fun link (t1 as Node (r, x1, c1), t2 as Node (_, x2, c2)) =
if Elem.leq(x1,x2) then Node(r+1,x1,t2 ::c1)
else Node(r+1,x2,t1 ::c2)
```
Связываем мы всегда деревья одного ранга.
Теперь определяем биномиальную кучу как коллекцию биномиальных
деревьев, каждое из которых имеет порядок кучи, и никакие два дерева не совпадают по рангу. Мы представляем эту коллекцию в виде списка деревьев в возрастающем порядке ранга.
```
Type Heap = Tree list
```
Поскольку каждое биномиальное дерево содержит 2^r элементов, и никакие два дерева по рангу не совпадают, деревья размера n в точности соответствуют единицам в двоичном представлении n. Например, число 21 в двоичном виде выглядит как 10101, и поэтому биномиальная куча размера 21 содержит одно дерево ранга 0, одно ранга 2, и одно ранга 4 (размерами, соответственно, 1, 4 и 16). Заметим, что так же, как двоичное представление n содержит не более log(n + 1) единиц, биномиальная куча размера n содержит не более log(n + 1) деревьев.
Теперь мы готовы описать функции, действующие на биномиальных деревьях. Начинаем мы с insert и merge, которые определяются примерно ана- логично сложению двоичных чисел. Чтобы внести элемент в кучу, мы сначала создаем одноэлементное дерево (т. е., биномиальное дерево ранга 0), затем поднимаемся по списку суще- ствующих деревьев в порядке возрастания рангов, связывая при этом одноранговые деревья. Каждое связывание соответствует переносу в двоичной арифметике.
```
fun rank (Node (r, x, c)) = r
fun insTree (t,[]) = [t]
| insTree (t, ts as t' :: ts') =
if rank t < rank t' then t :: ts else insTree (link (t, t'), ts')
```
```
fun insert (x, ts) = insTree (Node (0, x, []) , ts)
```
В худшем случае, при вставке в кучу размера n = 2k^1, требуется k связываний и O(k) = O(log n) времени.
При слиянии двух куч мы проходим через оба списка деревьев в порядке возрастания ранга и связываем по пути деревья равного ранга. Как и преж- де, каждое связывание соответствует переносу в двоичной арифметике.
```
fun merge (ts1 , []) =ts1
| merge ([], ts2)=ts2
| merge(ts1 as t1 ::ts'1, ts2 as t2 ::ts'2)=
if rank t1 < rank t2 then t1 :: merge (ts'1, ts2)
else if rank t2 < rank t1 then merge (ts1, ts'2)
else insTree (link (t1 , t2), merge (ts'1 , ts'2))
```
Функции findMin и deleteMin вызывают вспомогательную функцию removeMinTree, которая находит дерево с минимальным корнем, исключает его из списка
и возвращает как это дерево, так и список оставшихся деревьев.
```
fun removeMinTree [t] = (t, [])
| removeMinTree (t :: ts) =
let val (t ' , ts ') = removeMinTree ts
in if Elem.leq (root t, root t') then (t, ts) else (t', t :: ts') end
```
Функция findMin просто возвращает корень найденного дерева
```
fun findMin ts = let val (t , _) = removeMinTree ts in root t end
```
Функция deleteMin устроена немного похитрее. Отбросив корень найденного дерева, мы еще должны вернуть его потомков в список остальных деревьев. Заметим, что список потомков почти уже соответствует определению би номиальной кучи. Это коллекция биномиальных деревьев с неповторяющимися рангами, но только отсортирована она не по возрастанию, а по убыванию ранга. Таким образом, обратив список потомков, мы преобразуем его в биномиальную кучу, а затем сливаем с оставшимися деревьями.
```
fun deleteMin ts = let val (Node (_, x, ts1), ts2) = removeMinTree ts
in merge (rev ts1, ts2) end
```
Полная реализация биномиальных куч
```
functor BinomialHeap(Element: ORDERED) : Heap = struct
structure Elem = Element
datatype Tree = Node of int $\times$ Elem.T $\times$ Tree list
datatype Heap = Tree list
val empty = []
val isEmpty ts = null ts
fun rank (Node(r,x,c)) = r
fun root (Node(r,x,c)) = x
fun link ($t_1$ as Node ($r_1$,$x_1$,$c_1$), $t_2$ as Node ($r_2$,$x_2$,$c_2$)) =
if Elem.leq ($x_1$,$x_2$) then Node(r+1, $x_1$, $t_2$::$c_1$)
else Node(r+1, $x_2$, $t_1$::$c_2$)
fun insTree (t,[]) = [t]
| insTree (t, ts as t'::ts') =
if rank t < rank t' then t::ts else insTree(link(t,t'), ts')
fun insert (x,ts) = insTree(Node(0,x,[]), ts)
fun merge ($ts_1$, []) $=$ $ts_1$
| merge ([], $ts_2$) $=$ $ts_2$
| merge ($ts_1$ as $t_1$::$ts_1'$, $ts_2$ as $t_2$::$ts_2'$) =
if rank $t_1$ < rank $t_2$ then $t_1$ :: merge($ts_1$,$ts_2'$)
else if rank $t_2$ < rank $t_1$ then $t_2$ :: merge($ts_2$, $ts_1'$)
else insTree(link($t_1$,$t_2$), merge($ts_1'$,$ts_2'$)
fun removeMinTree [] = raise EMPTY
| removeMinTree [t] = (t,[])
| removeMinTree (t::ts) =
let val ($t'$, $ts'$) $=$ removeMinTree ts
in if Elem.leq (root t, root t') then (t,ts) else (t', t::ts') end
fun findMin ts = let val (t,_) = removeMinTree ts in root t end
fun deleteMin ts =
let val (Node(_, x,$ts_1$), $ts_2$) $=$ removeMinTree ts
in merge (rev $ts_1$,$ts_2$) end
end
```