За последние пятнадцать лет амортизация стала мощным инструментом в
построении и анализе структур данных. Реализации с амортизированными
характеристиками производительности часто оказываются проще и быстрее,
чем реализации со сравнимыми жёсткими характеристиками.
### Методы амортизированного анализа
Имея
последовательность операций, мы можем интересоваться временем, которое
отнимает вся эта последовательность, однако при этом нам может быть
безразлично время каждой отдельной операции. Например, имея $n$
операций, мы можем желать, чтобы время всей последовательности было
ограничено показателем `O(n)`, не настаивая, чтобы каждая из этих
операций происходила за время `O(1)`. Нас может устраивать, чтобы
некоторые из операций занимали `O(log n)` или даже `O(n)`, при
условии, что общая стоимость всей последовательности будет
`O(n)`. Такая дополнительная степень свободы открывает широкое
пространство возможностей при проектировании, и часто позволяет найти
более простые и быстрые решения, чем варианты с аналогичными жёсткими
ограничениями.
Чтобы доказать, что соблюдается амортизированное ограничение, нужно
определить амортизированную стоимость для каждой операции, и доказать,
что для любой последовательности операций общая амортизированная
стоимость является верхней границей общей реальной стоимости
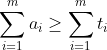
где `ai`- амортизированная стоимость операции `i`, `t_i` - ее
реальная стоимость, а `m` - общее число операций. Обычно
доказывается несколько более сильный результат: что на любой
промежуточной стадии в последовательности операций общая текущая
амортизированная стоимость является верхней границей для общей текущей
реальной стоимости.
Амортизация позволяет некоторым операциям быть дороже, чем их
амортизированная стоимость. Такие операции называются
**дорогими(expensive)**. Операции, для которых амортизированная стоимость превышает реальную, называются **дешевыми(cheap)**. Дорогие операции уменьшают текущие накопления, а дешевые их увеличивают. Главное при доказательстве амортизированных характеристик стоимости - показать, что дорогие
операции случаются только тогда, когда текущих накоплений хватает,
чтобы покрыть их дополнительную стоимость.
Существует два метода для анализа амортизированных структур данных:
0. метод банкира
0. метод физика
В методе банкира текущие накопления представляются как кредит(credits),
привязанный к определенным ячейкам структуры данных. Этот кредит
используется, чтобы расплатиться за будущие операции доступа к этим
ячейкам. Амортизированная стоимость операции определяется как ее
реальная стоимость плюс размер кредита, выделяемого этой операцией,
минус размер кредита, который она расходует
```
ai = ti + ci − c ̄ i
```
де `c_i`- размер кредита, выделяемого операцией `i`, а `c ̄ ` -
размер кредита, расходуемого операцией `i`. Каждая единица кредита
должна быть выделена, прежде чем израсходована, и нельзя расходовать
кредит дважды.
В методе физика определяется функция `Phi`, отображающая всякий
объект `d` на действительное число, называемое его
потенциалом(potential). Потенциал обычно выбирается так, чтобы
изначально равняться нулю и оставаться неотрицательным. В таком случае
потенциал представляет нижнюю границу текущих накоплений.
Пусть объект `di` будет результатом операции `i` и аргументом
операции `i+1`. Тогда амортизированная стоимость операции `i`
определяется как сумма реальной стоимости и изменения потенциалов между
`di-1` и `di`, т.е.,
```
ai = ti + Phi(di) - Phi(di-1)
```
### Очереди
Самая распространенная чисто функциональная реализация очередей
представляет собой пару списков, `f` и `r`, где `f` содержит головные элементы очереди в правильном порядке, а r состоит из хвостовых элементов в обратном порядке.
Например, очередь, содержащая целые числа 1...6, может быть
представлена списками `f=[1,2,3]` и
`r=[6,5,4]`. Это представление можно описать следующим
типом:
```
type alpha Queue = alpha list x alpha list
```
В этом представлении голова очереди - первый элемент `f`,
так что функции `head` и `tail`
возвращают и отбрасывают этот элемент, соответственно.
```
fun head (x :: f, r) = x
fun tail (x :: f, r) = f
```
Подобным образом, хвостом очереди является первый элемент
`r`, так что `snoc` добавляет к `r` новый элемент.
```
fun snoc ((f,r), x) = (f, x :: r)
```
Элементы добавляются к `r` и убираются из `f`, так
что они должны как-то переезжать из одного списка в другой. Этот
переезд осуществляется путем обращения `r` и установки его
на место`f` всякий раз, когда в противном случае
`f` оказался бы пустым. Одновременно `r`
устанавливается в `[]`. Наша цель - поддерживать
инвариант, что список `f` может быть пустым только в том
случае, когда список `r` также пуст (т.е., пуста вся
очередь). Заметим, что если бы `f` был пустым при непустом
`r`, то первый элемент очереди находился бы в конце
`r`, и доступ к нему занимал бы `O(n)` времени. Поддерживая
инвариант, мы гарантируем, что функция `head` всегда может
найти голову очереди за `O(1)` времени.
### Расширяющиеся деревья}{splay trees}
Возможно, самая известная
и успешно применяемая амортизированная структура данных. Расширяющиеся
деревья являются ближайшими родственниками двоичных сбалансированных
деревьев поиска, но они не хранят никакую информацию о балансе
явно. Вместо этого каждая операция перестраивает дерево при помощи
некоторых простых преобразований, которые имеют тенденцию увеличивать
сбалансированность. Несмотря на то, что каждая конкретная операция
может занимать до `O(n)` времени, амортизированная стоимость ее не превышает `O(log n)`.
Важное различие между расширяющимися деревьями и сбалансированными
двоичными деревьями поиска вроде красно-чёрных деревьев из состоит в том, что расширяющиеся деревья перестраиваются даже во время запросов (таких, как `member`), а не только во время обновлений (таких, как `insert`).
Это свойство мешает использованию расширяющихся деревьев для реализации
абстракций вроде множеств или конечных отображений в чисто
функциональном окружении, поскольку приходилось бы возвращать в
запросе новое дерево наряду с ответом на запрос.
Однако в некоторых абстракциях операции-запросы достаточно ограничены,
чтобы эту проблему можно было обойти. Хорошим примером служит
абстракция кучи, поскольку здесь единственным интересным запросом
является `findMin`. Как мы увидим, расширяющиеся деревья дают
нам отличную реализацию кучи.
Представление расширяющихся деревьев идентично представлению
несбалансированных двоичных деревьев поиска.
```
datatype Tree = E | T of Tree × Elem.T × Tree
```
Однако в отличие от несбалансированных двоичных деревьев поиска, мы позволяем дереву содержать повторяющиеся
элементы. Эта разница не является фундаментальным различием расширяющихся
деревьев и несбалансированных двоичных деревьев поиска; она просто
отражает отличие абстракции множества от абстракции кучи.
Рассмотрим следующую стратегию реализации для`insert`:
разобьем существующее дерево на два поддерева, чтобы одно содержало все
элементы, меньше или равные новому, а второе все элементы, большие
нового. Затем породим новый узел из нового элемента и двух этих
поддеревьев. В отличие от вставки в обыкновенное двоичное дерево
поиска, эта процедура добавляет элемент как корень дерева, а не как
новый лист.
Однако при таком решении не делается никакой попытки перестроить
дерево, добиваясь лучшего баланса. Вместо этого мы применяем простую
эвристику для перестройки: каждый раз, пройдя по двум левым ветвям
подряд, мы проворачиваем два пройденных узла.

одна из тех структур, которые
сводят специалистов с ума. С одной стороны, их легко реализовать и они
весьма хорошо показали себя на практике. С другой стороны, провести их
полный анализ не удается уже более 10 лет!
Парные кучи представляют собой упорядоченные по принципу кучи деревья
с переменной степенью ветвления; их можно определить следующим типом
данных:
```
datatype Heap = E | T of Elem.T × Heap list
```
Мы считаем правильными только такие деревья, где `E` никогда
не встречается в качестве ребенка вершины `T`.
Парные деревья называются именно так благодаря операции
`deleteMin`. Эта операция отбрасывает корень, а затем
сливает деревья в два прохода. Первый проход сливает деревья парами
слева направо (т.е., первое дерево сливается со вторым, третье с
четвертым и т.д.). При втором проходе получившиеся деревья сливаются
справа налево.
## Избавление от амортизации
Чаще всего нас не интересует, являются ли ограничения, соблюдаемые
структурой, жёсткими или амортизированными; основные критерии для
выбора одной структуры данных вместо другой - общая эффективность и
простота реализации (возможно, ещё наличие исходного кода). Однако в
некоторых прикладных областях оказывается важно ограничить время
выполнения отдельных операций, а не их последовательностей. В
этих случаях структура с жёсткими ограничениями часто предпочтительнее
структуры с амортизированными характеристиками, даже если
амортизированная структура в целом проще и быстрее.
* Системы реального времени. В системах реального времени
предсказуемость важнее голой скорости. Если
из-за дорогой операции система пропустит жёсткий
предельный срок, неважно будет, сколько дешёвых операций завершилось
раньше назначенного времени.
* Параллельные системы. Если один процессор в синхронной
системе выполняет дорогую операцию в то время, как остальные
выполняют дешёвые, то остальным процессорам придётся ждать, пока
закончит работу самый медленный.
* Диалоговые системы. Диалоговые системы подобны системам
реального времени - для пользователей предсказуемость часто
важнее, чем чистая скорость. Например,
пользователи могут предпочесть 100 ответов с задержкой 1 секунда
варианту с 99 ответами при задержке 0.25 секунд и одним ответом с
задержкой 25 секунд, даже при том, что второй из этих сценариев
вдвое быстрее.
### Расписания
Метод для преобразования амортизированных структур данных в структуры с жёсткими ограничениями путем систематического вынуждения задержек, так что ни
одна из них не выполняется слишком долго. При использовании этого
метода к каждому объекту добавляется дополнительная компонента - **расписание(schedule)**, управляющая порядком вынуждения задержек
внутри этого объекта.
Амортизированные структуры данных и структуры данных с жёсткими
ограничениями различаются в основном временем, когда происходит вычисление,
входящее в стоимость какой-либо операции. В структуре с жёсткими ограничениями для
наихудшего случая все вычисления, составляющие стоимость операции,
происходят во время самой этой операции. В амортизированной структуре
данных некоторые вычисления, входящие в стоимость операции, могут на
самом деле производиться во время более поздних операций. Отсюда мы
видим, что почти все структуры данных, считающиеся жёсткими, будучи
реализованы на чисто ленивом языке, превращаются в амортизированные,
поскольку многие вычисления оказываются задержаны без особой нужды.
Следовательно, для описания структур с жёсткими ограничениями нам
нужен энергичный язык. Если же нам нужно описывать как
амортизированные, так и жёсткие структуры данных, требуется язык,
поддерживающий как ленивый порядок вычисления, так и
энергичный. Имея такой язык, мы можем рассмотреть любопытный
гибридный подход: структуры с жёсткими характеристиками, использующие
внутри своей реализации ленивое вычисление. Мы получаем такие
структуры данных, беря за основу ленивые амортизированные структуры и
модифицируя их так, чтобы каждая операция укладывалась в отведенное ей
время.
В ленивой амортизированной структуре данных каждая конкретная операция
может занять дольше, чем её заявленное ограничение. Однако такое
происходит только в том случае, если эта операция вынуждает задержку,
которая уже была оплачена, но требует большого времени для
выполнения. Чтобы уложиться в жёсткие ограничения, мы должны
гарантировать, что всякая задержка выполняется не дольше отведенного
ей времени.
Определим **собственную стоимость(intrinsic cost)** задержки как
время, которое уходит на вынуждение задержки в предположении, что все
другие задержки, от которых она зависит, уже были вынуждены и
мемоизированы, и, следовательно, занимают по `O(1)` времени
каждая. (Это определение похоже на определение нераздельной стоимости
операции.) Первым шагом в преобразовании амортизированной структуры в
жёсткую будет уменьшение собственной стоимости каждой
задержки до размеров меньше желаемого ограничения. Обычно при этом
требуется переписать дорогие монолитные функции и сделать их
пошаговыми - либо путем небольших изменений в алгоритмах, либо путем
перехода от представления, поддерживающего только монолитные функции,
скажем, задержанных списков, к такому, которое также поддерживает
пошаговые функции, скажем, к потокам.
Даже если каждая задержка имеет маленькую собственную стоимость,
некоторые задержки по-прежнему могут занимать долгое время. Это
происходит, когда одна задержка зависит от другой, эта вторая от
третьей, и так далее. Если ни одна из этих задержек заранее не была
выполнена, то вынуждение первой задержки приводит к каскаду других
вынуждений.
Случалось ли вам ставить костяшки домино в ряд, чтобы каждая из них
сбивала следующую? Несмотря на то, что собственная стоимость опрокидывания
каждой костяшки равна `O(1)`, реальная стоимость опрокидывания первой
костяшки может быть намного, намного больше.
Второй шаг при преобразовании амортизированной структуры данных в
жёсткую - избежать каскадирования вынуждений, устроив так, чтобы
всякий раз при вынуждении задержки все другие задержки, от которых она
зависит, были уже вынуждены и мемоизированы. Тогда ни одна задержка не
занимает при выполнении больше, чем её собственная стоимость. Мы этого
добиваемся, строя систематическое расписание(schedule)
выполнений каждой задержки, чтобы все они были готовы к тому времени,
как нам понадобятся. Трюк здесь состоит в том, чтобы рассматривать
выплату долга буквально, и вынуждать каждую задержку в момент, когда
она оплачивается.
Работа с расписанием подобна опрокидыванию ряда костяшек начиная с
хвоста, так чтобы всякий раз, когда одна костяшка падает на другую,
эта другая была уже заранее сбита. Тогда реальная стоимость
опрокидывания каждой костяшки будет мала.